实验问题
单输入单输出系统:$A(z^{-1})y(t)=B(z^{-1})u(t)+C(z^{-1})e(t)$
其中:
\[\begin{matrix} A(z^{-1})=1-2.851z^{-1}+2.717z^{-2}-0.865z^{-3} \\ B(z^{-1})=z^{-1}+z^{-2}+z^{-3} \\ C(z^{-1})=1+0.7z^{-1}+0.7z^{-1}+0.22z^{-2} \\ e(t) \sim N(0,1) \end{matrix}\]- 产生必要随机数;
- 设计实验,产生输出数据;
- 用最小二乘辨识系统模型;
- 任用一种适合有色噪声辨识算法辨识系统模型。
实验原理
递推最小二乘
递推最小二乘辨识算法可减少运算量和数据在计算机中所占的存储量,同时也能实时辨识出系统的特性,将最小二乘转化为递推估计。最小二乘递推算法RLS的基本思想是
\[\widehat{\theta}_{new}(k) = \widehat {\theta }_{old}(k-1)+F_{fix}\]其中$\widehat{\theta}_{new}(k)$是新的估计值,
$\widehat{\theta}_{old}(k-1)$是旧的估计值,
$F_{fix}$ 是修正项
算法迭代方程为
\[\left\{ \begin{aligned} \widehat{\theta}(k)&= \widehat{\theta}(k-1) +K(k)[z(k)-h^{T}(k)\widehat{\theta}(k-1)]\\ K(k)&=P(k-1)h(k)[h^T(k)P(k-1)h(k)+1]^{-1}\\ P(k)&=P(k-1)-K(k)h^T(k)P(k-1) \end{aligned} \right.\]增广最小二乘
增广最小二乘递推算法,扩充了最小二乘法的参数向量$\theta$和数据向量$h(k)$的维数,把噪声模型的辨识同时考虑进去,因此被称为增广最小二乘法。最小二乘法的许多结论对它都是适用的,但最小二乘法只能获得模型的参数估计。如果噪声模型必须用$D(z^{-1}v(k))$表示时,只能用RELS算法,方可获得无偏估计,这是RLS算法所不能代替的。
考虑SISO 的动态系统,输入$u(k)$和输出$z(k)$是可以观测的;$G(z^{-1})$是系统模型,用来描述系统的输入输出特性,$y(k)$是系统的实际输出。$N(z^{-1})$是噪声模型,$v(k)$是均值为零的不相关随机噪声。通常
\[G(z^{-1})= \begin{aligned} B(z^{-1})\\ A(z^{-1}) \end{aligned} ,N(z^{-1})= \begin{aligned} D(z^{-1})\\ C(z^{-1}) \end{aligned}\]式中
\[\left\{ \begin{aligned} A(z^{-1})&=1+a_1z^{-1}+a_2z^{-2}+ ... +a_{n_a}z^{-n_a} \\ B(z^{-1})&=b_1z^{-1}+b_2z^{-2}+ ... +b_{n_b}z^{-n_b} \end{aligned} \right.\] \[\left\{ \begin{aligned} A(z^{-1})&=1+a_1z^{-1}+a_2z^{-2}+ ... +a_{n_a}z^{-n_a} \\ B(z^{-1})&=b_1z^{-1}+b_2z^{-2}+ ... +b_{n_b}z^{-n_b} \end{aligned} \right.\]若SISO 系统采用平均滑动模型,即
\[\begin{matrix} C(z^{-1})=A(z^{-1}) \\ A(z^{-1})z(k)=B(z^{-1})u(k)+D(z^{-1})v(k) \end{matrix}\]若假定模型阶次$n_a$ 、$n_b$ 、$n_d$已经确定,则这类问题的辨识可用增广最小二乘法,以便获得满意的结果。令
\[\left\{ \begin{aligned} \theta &= [a_1,a_2,...,a_{n_a},b_1,b_2,...,b_{n_b},d_1,d_2,...,d_{n_d}]^T \\ h{k}&=[-z(k-1),...,-z(k-n_{n_a}),u(k-1),...,u(k-n_b),v(k-1),...,v(k-n_d)]^T \end{aligned} \right.\]将模型3化为最小二乘格式
\[z(k)=h^T(k)\theta + v(k)\]由于$v(k)$是白噪声,所以利用最小二乘法即可获得参数$\theta$的无偏估计。但是数据向量$h(k)$中包含着不可测的噪声量$v(k-1),…,v(k-n_d)$,它可用相应的估计值替代。置
\[h(k)=[-z(k-1),...,-z(k-n_a),u(k-1),...,u(k-n_b),v(k-1),...,v(k-n_d)]^T\]式中,$\widehat{v}(k)=0,k\leq0$;当$k>0$时,
\[\widehat{v}(k)=z(k)-h^T(k)\widehat{\theta}(k-1)\]或
\[\widehat{v}(k)=z(k)-h^T(k)\widehat{\theta}(k)\]如果$\frac{1}{\Lambda}=1$,即所有采样数据都是等同加权时,增广最小二乘递推算法RELS可以写为
\[\left\{ \begin{aligned} \widehat{\theta}(k)&=\widehat{\theta}(k-1)+K(k)[z(k)-h^T(k)\widehat{\theta}(k-1)]\\ K(k)&=P(k-1)h(k)[h^T(k)P(k-1)h(k)+1]^{-1} \\ P(k)&=[1-K(k)h^T(k)]P(k-1) \end{aligned} \right.\]实验过程
产生白噪声和m序列
白噪声序列$e(t)$可由乘同余法自己编写函数实现,也可以由matlab自带的randn函数产生,本实验采用randn函数产生;系统的输入$u(t)$选择m序列,其级数为4,初相为$\left[ \begin{matrix} 1&1&1&0 \end{matrix} \right]$,本原多项式为$f(x)=x^4+x^3+1$。
产生输出采样信号
考虑噪声对输出的影响,则系统输出为
\[\begin{array}{lr} z(k)&=2.851z(k-1)-2.717z(k-2)+0.865z(k-3)+u(k-1)\\ &+u(k-2)+u(k-3)+v(k)+0.7v(k-1)+0.22v(k-2) \end{array}\]递推最小二乘辨识
给被辨识参数$\theta$和$P$赋初值。根据1式计算$K(k)$、$\theta(k)$、$P(k)$,当参数收敛满足要求时停止迭代计算,输出辨识结果。
增广最小二乘辨识
给被辨识参数$\theta$和$P$赋初值。根据11式计算$K(k)$、$\theta(k)$、$P(k)$,当参数收敛满足要求时停止迭代计算,输出辨识结果。
实验结果与分析
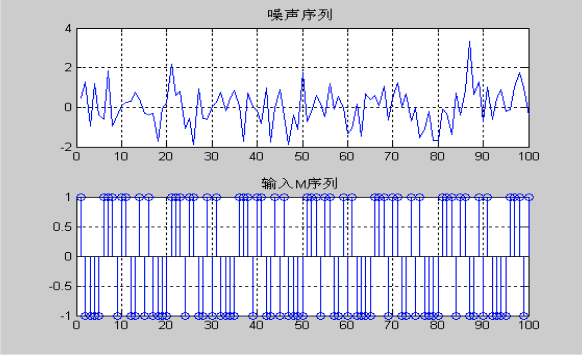
系统白噪声和系统输入m序列
系统白噪声和系统输入m序列如图1所示。
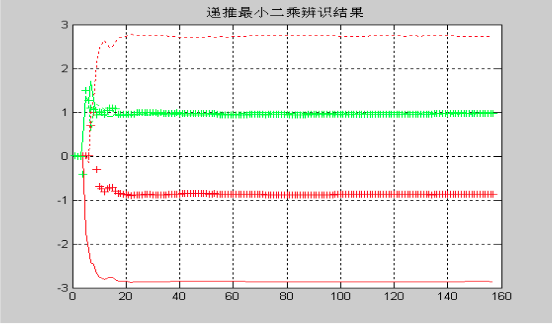
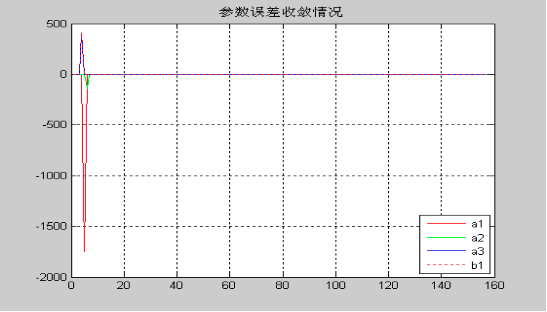
采用递推最小二乘辨识算法
实验时,给定辨识精度为E=0.00005,m序列信号峰峰大小为10,经过157次迭代,达到给定经度。此时辨识结果为
\[\begin{matrix} a_1=-2.8599&a_2=2.7339&a_3=-0.8731 \\ b_1=0.9875&b_2=0.9681 &b_3=0.9705 \end{matrix}\]在实验时,对于m序列,其峰峰值越大,辨识的参数与真值误差越小。
增广最小二乘辨识
实验时,给定辨识精度为E=0.00005,m序列峰峰值为2,经过40次迭代达到给定经度,此时辨识结果为
\(\begin{matrix}
a_1=-2.851&a_2=2.7217&a_3=-0.865 \\
b_1=1&b_2=1 &b_3=1 \\
c_1=1&c_2=0.7&c_3=0.22
\end{matrix}\)
增广最小二乘的仿真结果如图4和图5所示。
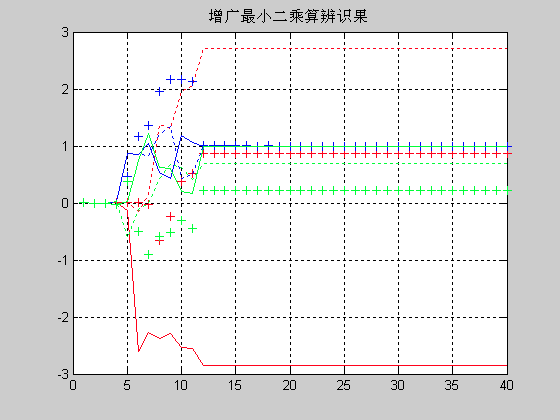
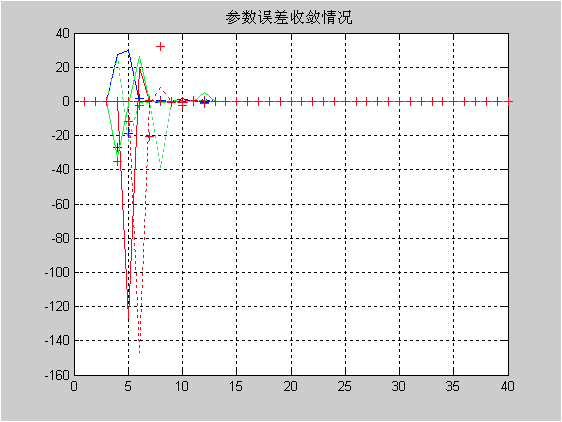
参数的真值和估计值如表所示:
| 参数真值 | 递推最小二乘辨识 | 增广最小二乘辨识 | |
|---|---|---|---|
| $a_1$ | -2.851 | -2.8599 | -2.8510 |
| $a_2$ | 2.717 | 2.7339 | 2.7170 |
| $a_3$ | -0.865 | -0.8731 | -0.8650 |
| $b_1$ | 1.000 | 0.9875 | 1.0000 |
| $b_2$ | 1.000 | 0.9681 | 1.0000 |
| $b_3$ | 1.000 | - | 1.0000 |
| $c_1$ | 1.000 | - | 1.0000 |
| $c_2$ | 0.700 | - | 0.7000 |
| $c_3$ | 0.220 | - | 0.2200 |
从表格对比可以看到,增广最小二乘考虑了噪声模型,与递推最小二乘算法相比,速度快、辨识结果精确,而且可以得到噪声模型参数。
附录
递推最小二乘辨识matlab仿真程序
clear
L=200;
y1=1;y2=1;y3=1;y4=0;
for i=1:L
x1=xor(y3,y4);
x2=y1;x3=y2;x4=y3;
y(i)=y4;
if y(i)>0.5
u(i)=-5;
else
u(i)=5;
end
y1=x1;y2=x2;y3=x3;y4=x4;
end
figure(1)
i=1:20;
stem(u(i));
grid on;
v=1*randn(L,1);
z(3)=0;z(2)=0;z(1)=0;
for k=4:L
z(k)=2.851*z(k-1)-2.717*z(k-2)+0.865*z(k-3)+u(k-1)
+u(k-2)+u(k-3)+v(k)+0.7*v(k-1)+0.22*v(k-2);
end
c0=[0.001 0.001 0.001 0.001 0.001 0.001]';
p0=10^3*eye(6,6);
E=0.000005;
c=[c0,zeros(6,L-1)];
e=zeros(6,L);
for k=4:L
h1=[-z(k-1),-z(k-2),-z(k-3),u(k-1),u(k-2),u(k-3)]';
k1=p0*h1*inv(h1'*p0*h1+1);
c1=c0+k1*(z(k)-h1'*c0);
e1=c1-c0;
e2=e1./c0;
e(:,k)=e2;
c0=c1;
c(:,k)=c1;
p1(:,:,k)=p0-k1*k1'*[h1'*p0*h1+1];
p0=p1(:,:,k);
if abs(e2)<=E
N=k;
break;
end
N=k;
end
a1=c(1,1:N); a2=c(2,1:N); a3=c(3,1:N);b1=c(4,1:N);
b2=c(5,1:N);b3=c(6,1:N);
ea1=e(1,:); ea2=e(2,:);ea3=e(3,:);
eb1=e(4,:); eb2=e(5,:); eb3=e(6,:);
i=1:N;
figure(2)
plot(i,a1,'r',i,a2,'r:',i,a3,'r+',i,b1,'g',i,b2,'g:',i,b3,'g+');
grid on;
figure(3)
i=1:30;
plot(i,ea1(1:30),'r',i,ea2(1:30),'g',i,eb1(1:30),'b',i,eb2(1:30),'r:');
grid on;
legend('a1','a2','a3','b1','b2','b3');
增广最小二乘的matlab仿真程序
clear all;
clc;
L=100;
y1=1;y2=1;y3=1;y4=0;
for i=1:L
x1=xor(y3,y4);
x2=y1;
x3=y2;
x4=y3;
y(i)=y4;
if y(i)>0.5
u(i)=-1;
else
u(i)=1;
end
y1=x1;y2=x2;y3=x3;y4=x4;
end
v=1*randn(1,L);
z(3)=0;z(2)=0;z(1)=0;
for k=4:L
z(k)=2.851*z(k-1)-2.717*z(k-2)+0.865*z(k-3)+u(k-1)
+u(k-2)+u(k-3)+v(k)+0.7*v(k-1)+0.22*v(k-2);
end
figure(1);subplot(2,1,2);
stem(u),grid on;
subplot(2,1,1);plot(v),grid on;
c0=[0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001]';
p0=10^6*eye(9,9);
E=5e-10; c=[c0,zeros(9,L-1)];
e=zeros(9,L);N=L+1;
for k=4:L
h1=[-z(k-1),-z(k-2),z(k-3),u(k-1),u(k-2),u(k-3),v(k),v(k-1),v(k-2)]';
k1=p0*h1*inv(h1'*p0*h1+1);
c1=c0+k1*(z(k)-h1'*c0);
e1=c1-c0;
e2=e1./c0;
e(:,k)=e2;
c0=c1;
c(:,k)=c1;
p1(:,:,k)=p0-k1*k1'*[h1'*p0*h1+1];
p0=p1(:,:,k);
if abs(e2)<=E
N=k;
break;
end
end
if N~=L+1
a1=c(1,1:N); a2=c(2,1:N); a3=c(3,1:N);
b1=c(4,1:N); b2=c(5,1:N);b3=c(6,1:N);
d1=c(7,1:N); d2=c(8,1:N); d3=c(9,1:N);
ea1=e(1,1:N); ea2=e(2,1:N); ea3=e(3,1:N);
eb1=e(4,1:N); eb2=e(5,1:N);eb3=e(6,1:N);
ed1=e(7,1:N); ed2=e(8,1:N); ed3=e(9,1:N);
figure(2);
i=1:N;
plot(i,a1,'r',i,a2,'r:',i,a3,'r+',i,b1,'b',i,b2,'b:',
i,b3,'b+',i,d1,'g',i,d2,'g:',i,d3,'g+');
grid on;
figure(3);
plot(i,ea1,'r',i,ea2,'r:',i,ea3,'r+',i,eb1,'b',i,eb2,'b:',
i,eb3,'b+',i,ed1,'g',i,ed2,'g:',i,ed3,'r+');
grid on;
end